Program for Fibonacci numbers

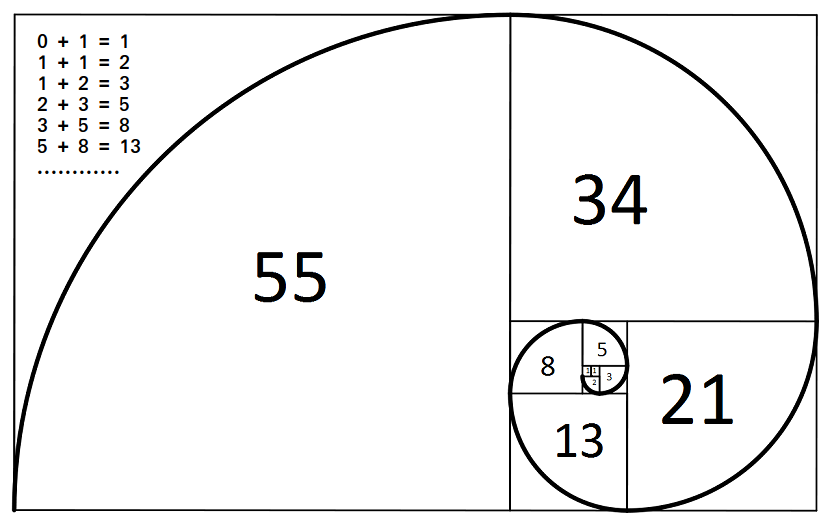
The Fibonacci numbers are the numbers in the following integer sequence.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …….

In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
Fn = Fn-1 + Fn-2
with seed values
F0 = 0 and F1 = 1

Give a number n, print n-th Fibonacci Number.

Input:    n = 2

Output: 1

Input:    n = 7

Output: 13

Write a function int fib(int n) that returns Fn. For example, if n = 0, then fib() should return 0. If n= 1, then it should return 1. For n > 1, it should return Fn-1 + Fn-2.

Program:

Method -1 (Use recursion)

# Function for nth Fibonacci number def Fibonacci(n):     if n<0:         print("Incorrect input")     # First Fibonacci number is 0     elif n==1:         return 0     # Second number is 1Fibonacci     elif n==2:         return 1     else:         return Fibonacci(n-1)+Fibonacci(n-2) # Driver Program print(Fibonacci(7))

Time Complexity: T(n) = T(n-1) + T(n-2) which is exponential.

We observe that this implementation does a lot of repeated work. So, this will be some bad implementation.

Method -2 (Use Dynamic Programming)

# Fibonacci Series using Dynamic Programming

def fibonacci(n):

# Taking 1st two fibonacci nubers as 0 and 1

FibArray = [0, 1]

while len(FibArray) < n + 1: 

FibArray.append(0) 

if n <= 1:

return n

else:

if FibArray[n - 1] == 0:

FibArray[n - 1] = fibonacci(n - 1)

if FibArray[n - 2] == 0:

FibArray[n - 2] = fibonacci(n - 2)

FibArray[n] = FibArray[n - 2] + FibArray[n - 1]

return FibArray[n]

print(fibonacci(7))